新課標2011年高考考試說明——數學（理）(4)

　　（十三）不等式

　　1．不等關系

　　了解現實世界和日常生活中的不等關系，了解不等式（組）的實際背景.

　　2．一元二次不等式

　　（1） 會從實際情境中抽象出一元二次不等式模型.

　　（2） 通過函數圖像了解一元二次不等式與相應的二次函數、一元二次方程的聯系.

　　（3） 會解一元二次不等式，對給定的一元二次不等式，會設計求解的程序框圖.

　　3．二元一次不等式組與簡單線性規劃問題

　　（1） 會從實際情境中抽象出二元一次不等式組.

　　（2） 了解二元一次不等式的幾何意義，能用平面區域表示二元一次不等式組.

　　（3） 會從實際情境中抽象出一些簡單的二元線性規劃問題，并能加以解決.

　　4．基本不等式：

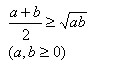
　　（1） 了解基本不等式的證明過程.

　　（2） 會用基本不等式解決簡單的最大（小）值問題.

　　（十四）常用邏輯用語

　　（1） 理解命題的概念.

　　（2）了解“若p，則q”形式的命題及其逆命題、否命題與逆否命題，會分析四種命題的相互關系.

　　（3） 理解必要條件、充分條件與充要條件的意義.

　　（4）了解邏輯聯結詞“或”、“且”、“非”的含義.

　　（5） 理解全稱量詞與存在量詞的意義.

　　（6） 能正確地對含有一個量詞的命題進行否定.

　　（十五）圓錐曲線與方程

　　（1） 了解圓錐曲線的實際背景，了解圓錐曲線在刻畫現實世界和解決實際問題中的作用.

　　（2） 掌握橢圓、拋物線的定義、幾何圖形、標準方程及簡單性質（范圍、對稱性、定點、離心率）.

　　（3） 了解雙曲線的定義、幾何圖形和標準方程，知道它的簡單幾何性質（范圍、對稱性、定點、離心率、漸近線）.

　　（4） 了解曲線與方程的對應關系

　　（5）理解數形結合的思想

　　（6）了解圓錐曲線的簡單應用.

　　（十六）空間向量與立體幾何

　　（1）了解空間向量的概念，了解空間向量的基本定理及其意義，掌握空間向量的正交分解及其坐標表示.

　　（2） 掌握空間向量的線性運算及其坐標表示.

　　（3） 掌握空間向量的數量積及其坐標表示，能用向量的數量積判斷向量的共線與垂直.

　　（4） 解直線的方向向量與平面的法向量.

　　（5） 能用向量語言表述線線、線面、面面的平行和垂直關系.

　　（6）能用向量方法證明有關直線和平面位置關系的一些定理（包括三垂線定理）.

　　（7） 能用向量方法解決直線與直線、直線與平面、平面與平面的夾角的計算問題，了解向量方法在研究幾何問題中的應用.

　　（十七）導數及其應用

　　（1）了解導數概念的實際背景.

　　（2） 通過函數圖像直觀理解導數的幾何意義.

　　（3） 根據導數的定義求函數

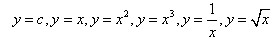
(c為常數)的導數.

　　（4） 能利用下面給出的基本初等函數的導數公式和導數的四則運算法則求簡單函數的導數，能求簡單的復合函數（僅限于形如f（ax+b）的復合函數）的導數.

·常見基本初等函數的導數公式和常用導數運算公式：

　　（5）了解函數單調性和導數的關系；能利用導數研究函數的單調性，會求函數的單調區間（其中多項式函數一般不超過三次）.

　　（6） 了解函數在某點取得極值的必要條件和充分條件；會用導數求函數的極大值、極小值（其中多項式函數一般不超過三次）；會求閉區間上函數的最大值、最小值（其中多項式函數一般不超過三次）.

　　（7）會用導數解決某些實際問題..

　　（8）了解定積分的實際背景，了解定積分的基本思想，了解定積分的概念.

　　（9） 了解微積分基本定理的含義.

　　（十八）推理與證明

　　（1）了解合情推理的含義，能利用歸納和類比等進行簡單的推理，了解合情推理在數學發現中的作用.

　　（2） 了解演繹推理的含義，了解合情推理和演繹推理的聯系和差異；掌握演繹推理的“三段論”，能運“三段論”進行一些簡單的演繹推理.

　　（3） 了解直接證明的兩種基本方法：分析法和綜合法；了解分析法和綜合法的思考過程、特點.

　　（4） 了解反證法的思考過程和特點.

　　（5）了解數學歸納法的原理，能用數學歸納法證明一些簡單的數學命題.

　　（十九）數系的擴充與復數的引入

　　（1）理解復數的基本概念，理解復數相等的充要條件.

　　（2）了解復數的代數表示法及其幾何意義；能將代數形式的復數在復平面上用點或向量表示，并能將復平面上的點或向量所對應的復數用代數形式表示.

　　（3）能進行復數代數形式的四則運算，了解兩個具體復數相加、相減的幾何意義．

　　（二十）計數原理

　　（1）理解分類加法計數原理和分步乘法計數原理，能正確區分“類”和“步”，并能利用兩個原理解決一些簡單的實際問題．

　　（2）理解排列的概念及排列數公式，并能利用公式解決一些簡單的實際問題.

　　（3）理解組合的概念及組合數公式，并能利用公式解決一些簡單的實際問題.

　　（4）會用二項式定理解決與二項展開式有關的簡單問題.

　　（二十一）概率與統計

　　（1） 理解取有限個值的離散型隨機變量及其分布列的概念，認識分布列刻畫隨機現象的重要性，會求某些取有限個值的離散型隨機變量的分布列.

　　（2）了解超幾何分布及其導出過程，并能進行簡單的應用.

　　（3） 了解條件概率的概念，了解兩個事件相互獨立的概念，理解n次獨立重復試驗的模型及二項分布，并能解決一些簡單的實際問題.

　　（4） 理解取有限個值的離散型隨機變量均值、方差的概念，會求簡單離散型隨機變量的均值、方差，并能利用離散型隨機變量的均值、方差概念解決一些簡單問題.

　　（5） 借助直觀直方圖認識正態分布曲線的特點及曲線所表示的意義.

　　（6）了解回歸的基本思想、方法及其簡單應用.

　　（7）了解獨立性檢驗的思想、方法及其初步應用.

　　二、選考內容與要求

　　（一）幾何證明選講

　　（1）理解相似三角形的定義與性質，了解平行截割定理.

　　（2）會證明和應用以下定理：①直角三角形射影定理；②圓周角定理；③圓的切線判定定理與性質定理；④相交弦定理；⑤圓內接四邊形的性質定理與判定定理；⑥切割線定理.

　　（二）坐標系與參數方程

　　（1）了解坐標系的作用，了解在平面直角坐標系伸縮變換作用下平面圖形的變化情況.

　　（2） 了解極坐標的基本概念，會在極坐標系中用極坐標刻畫點的位置，能進行極坐標和直角坐標的互化.

　　（3） 能在極坐標系中給出簡單圖形（如過極點的直線、過極點或圓心在極點的圓）表示的極坐標方程.

　　（4）了解參數方程，了解參數的意義.

　　（5） 能選擇適當的參數寫出直線、圓和圓錐曲線的參數方程.

　　（三）不等式選講

　　（1）理解絕對值的幾何意義，并能利用含絕對值不等式的幾何意義證明以下不等式：

　　∣a＋b∣≤∣a∣＋∣b∣；

　　∣a－b∣≤∣a－c∣＋∣c－b∣；

　　（2）會利用絕對值的幾何意義求解以下類型的不等式：

　　∣ax＋b∣≤c；

　　∣ax＋b∣≥c；

　　∣x－c＋∣x－b∣≥a

　　（3）通過一些簡單問題了解證明不等式的基本方法：比較法、綜合法、分析法